感知机(亦称感知器)是一种最简单的机器学习模型, 它可以用来解决线性分类问题, 是其它多种机器学习算法的基础, 很多文章在讲述感知机的时候往往使用类似如下所示的图片

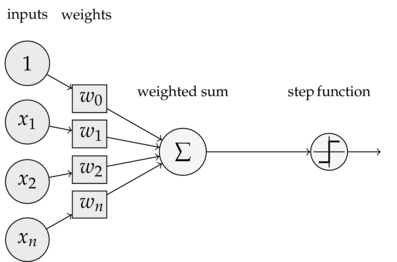
并直接指出最左侧的输入为权值向量, 常数 $\omega_0$ 为偏置, step function 为激活函数, 这样的描述方式并没有阐述感知机的本质, 反而容易给读者带来更多的困惑, 本文通过单纯的数学角度来描述感知机, 并给出所有涉及公式的详细推导

2.1 感知机的本质

分类问题是从群体中将具有相同或相似特征的个体划分为一个类别, 二分类是最简单的分类问题, 即将群体(即样本空间中的样本点)划分为两个类别, 对应到现实场景中例如给定 N 张人像照片, 将这 N 张人像图片划分为两组, 其中男性一组, 女性一组, 便是一个典型的二分类问题, 要通过程序来解决分类问题, 首先的一步便是对个体进行特征提取, 从数学观点来看, 这个过程相当于是将现实世界中的一个个体映射到一个向量(特征)空间中, 例如我们可以选定高矮、胖瘦、长发短发这 3 个特征来描述一个个体, 对于长发、高、瘦的人来说, 可以用如下的一个特征向量来描述(我们约定长发用 1 表示, 短发用 0 表示; 高用 1 表示, 矮用 0 表示; 胖用 1 表示, 矮用 0 表示)

$$A = [1, 1, 0] \tag{2.1}$$

这样以来, 每一个个体都可以用一个 3 维向量来描述, (特征)向量所在的空间我们一般称之为特征空间, 每个个体自然地对应到特征空间的一个点, 如此以来我们便可以使用数学方法对问题进行处理, 因此在接下来的讨论中, 我们抛去问题的实际背景, 仅仅从数学角度来讨论感知机. 感知机的本质是一个函数, 它是定义在一个「相同维度的向量集合」上的函数, 它的值域是 {-1, 1}, 可以用如下的一个抽象表达式来描述

$$f(N维向量集合) = ε, 其中 ε \in \{-1,1\} \tag{2.2}$$

但并非所有满足上式的 $f$ 都是感知机, 感知机本身是一个线性函数, 假定输入向量集合为 N 维向量集合, 则感知机的具体表达式为

$$f = sign(\vec\omega \cdot \vec x + b) \tag{2.3}$$

其中 $sign$ 为符号函数, $sign(x) = 1$ 当且仅当 $x \geq 0$, 否则 $sign(x) = -1$, 如果觉得向量形式不太直观, 可以将其拆开用多项式函数的形式来表达, 上式也可以写成

$$f = sign(Ax + By +Cz +....+ b), 其中 A、B、C .. b 为常数 \tag{2.4}$$

这里 $[x, y, z,...]^T$ 即对应 $2.3$ 式中的向量 $\vec x$, 而 $[A, B, C ...]$ 即对应 $2.3$ 式中的向量 $\vec \omega$, 其中 $b$ 为一个常实数, 到这里我们可以看到感知器的本质是一个线性多项式函数与符号函数构成的复合函数, 它的取值只有 $-1$ 和 $1$ 两个值, 它将 $N$ 维向量映射到 $\{-1, 1\}$ 上, 从而将向量划分为两类, 完成一个二分类任务, 一般来说分类问题可以划分成两类, 一类是线性分类问题, 另一类是非线性分类问题, 这里所谓的线性与非线性与代数里的线性定义是一致的, 如果一个分类器是参数的线性函数, 那么我们称该分类器为线性分类器, 否则便是非线性分类器, 从感知器函数的解析式可知, 感知器是一种线性分类器, 它可以用来解决线性二分类问题

2.2 感知机的几何意义

在感知机的表达式中, 输入向量的维度不是固定的, 如果我们令

$$Z = \vec \omega \cdot \vec x + b, 其中\vec \omega、 \vec x 为任意 N 维向量 \tag{2.5}$$

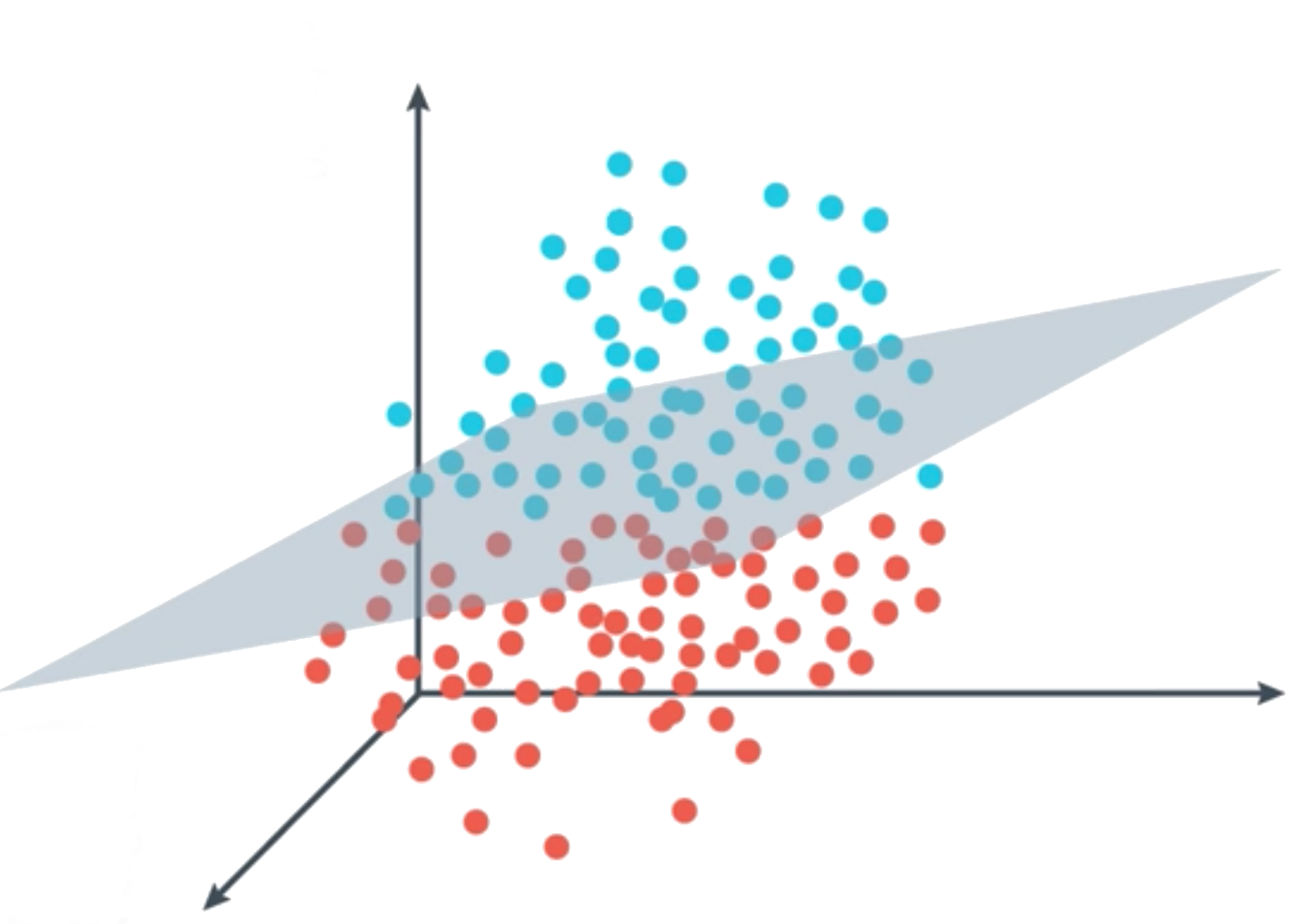
则感知机 $f$ 是 $Z$ 的泛函, 当 $Z$ 是一个二元函数时(即输入向量是一个二维向量), $Z$ 对应一条直线, 这条直线将二维欧氏空间划分为两部分, 当 $Z$ 是一个三元函数时, $Z$ 对应一个平面, 该平面将三维欧氏空间划分为两部分, 一般地, 当 $Z$ 是一个 $n$ 元函数时, Z 将 $n$ 维欧氏空间划分为两部分, 本质原因在于对于方程 $\vec\omega \cdot \vec x + b =0$, 我们取 $\vec\omega \cdot \vec x + b \gt 0$ 和 $\vec\omega \cdot \vec x + b \lt 0$ 便得到了整个 $n$ 维欧氏空间的所有点集, 在分类任务中, 我们所取的特征可能较多, 对应的特征向量的维度可能高于 3 维, 超出了人类所直观认识的维度空间, 这里我们将平面的说法延伸到高维空间, 当维度 $n \gt 3$ 时, 我们称方程

$$\vec \omega \cdot \vec x + b = 0 \tag{2.6}$$

所确定的点集为超平面, 例如方程 $2x + 3y + 4z + 5t = 0$ 就是一个三维超平面, 它可以将四维欧氏空间划分为两部分, 到这里我们可以知道, 感知机的几何意义便是一个 $n-1$ 维超平面, 它将 $n$ 维特征空间划分为两部分

2.3 感知机算法

感知机是一种线性分类器, 它只能处理线性分类问题, 因此感知机应用的对象必须是一个线性可分的数据集, 我们只考虑二分类的情形, 一般来说, 对于数据集中的每个数据, 我们通常用一个符号对 $(\vec x, y)$ 来表示, 其中 $\vec x$ 为输入, $y$ 为输出, 由于是二分类的问题, 因此我们可以约定 $y$ 的值域为 $\{-1, 1\}$, 所谓线性可分数据集, 即是存在线性函数 $f(\vec x)$, 使得对于该数据集中的任意一点, 都有 $f(\vec x) \cdot y \gt 0$, 从几何意义上我们也可以知道, 对于线性可分的数据集, 一定存在某个超平面可以将数据集中的点完全地划分在两侧, 由于实数的稠密性, 所以这样的超平面一定有无限多个, 这些超平面的集合便构成了感知机模型的集合, 到这里我们只是知晓了理论上的存在性, 关键的问题在于如何求出超平面的方程, 即如何获得一个感知器模型, 求解超平面方程的算法便是感知机算法, 从数学上讲, 这相当于是求解一个不定方程的一组解, 通过编程解决这个问题, 采用的思路往往是定义一个损失函数, 然后将该问题转换为一个极值问题通过迭代来解决, 所谓损失函数即是模型的输出与 $y$(标记值或真实值) 之间的某个距离度量函数, 在当前问题中, 一个显然的损失函数是误分类点的个数, 当误分类点个数为 0 时, 便得到了一组解, 我们可以尝试写一下这个损失函数的解析式, 我们首先定义误分类函数 $g$(其中 $f$ 为感知机函数)

$$g(\vec x) = \begin{cases} 1 & 当 f(\vec x) \cdot y \lt 0(即错误分类)\\ 0 & 当 f(\vec x) \cdot y \gt 0(即正确分类)\\ \end{cases} \tag{2.7}$$

有了误分类函数, 则损失函数 $h$ 可以定义为 $$h(\vec x) = \sum_{i=1}^{n} g(\vec x_i) \tag{2.8}$$

其中 $\vec x_i$ 为第 $i$ 个特征向量, $n$ 为特征向量总数, 观察 $(2.7)$ 和 $(2.8)$ 式我们可以知道, 函数 $h(x)$ 是不连续的函数, 进而也不可导, 这意味着我们无法使用微积分来处理这个函数的极值问题, 因此我们换一个思路, 重新定义损失函数, 另一个显然的度量误差的方式便是利用误分类点到超平面的距离之和, 当所有点都被正确分类以后, 该项指标的值也就最小化到 0 了, 我们首先给出点到超平面的欧氏距离公式, 先来看一个最简化的情形, 二维空间中的点到直线的欧氏距离公式,

$$d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}} \tag {2.9}$$

再来看, 三维空间中的点到二维平面的欧氏距离公式,

$$d = \frac{|Ax_0 + By_0 + Cz_0 +D|}{\sqrt{A^2 + B^2 + C^2}} \tag{2.10}$$

一般地, $n$ 维空间的点到 $n-1$ 维超平面($\vec \omega \cdot \vec x + b = 0$)的欧氏距离公式为

$$d = \frac{|\vec \omega \cdot \vec x_i + b|}{|\vec \omega|} \tag{2.11}$$

这里做一个小的额外补充说明, 「距离」在现实世界中是一个很显然的概念, 它似乎无需解释便可被理解, 但从广义上讲, 距离本身是一个公理化定义的概念, 凡是满足非负性(即 $d(x, y) \ge 0$)、对称性(即 $d(x, y) = d(y, x)$)以及三角不等式($d(x, z) \ge d(x,y) + d(y,z)$)的函数都为距离, 现实意义上通常所讲的欧氏距离只是距离的一种, 在这里我们使用欧氏距离, 因为对于当前的问题场景是最便于计算的, 除了欧氏距离外, 还有曼哈顿距离、闵氏距离、切比雪夫距离等, 在上面的 $(2.9)$ ~ $(2.11)$ 中, 分母的含义是权值向量的模, 这里也可以用向量的范数来表达, 在数值上, 向量长度的大小(即向量的模)等于它的 $L_2$ 范数, 因此 $(2.11)$ 式也可以写成

$$d = \frac{|\vec \omega \cdot \vec x_i + b|}{||\vec \omega||_2} \tag{2.12}$$

至此我们可以得到基于误分类点到超平面的欧氏距离之和的损失函数的解析式

$$h(\vec x) = \sum_{x_i \in M} \frac{|\vec \omega \cdot \vec x_i + b|}{||\vec \omega||_2} \tag{2.13}$$

由于损失函数的解析式中包含绝对值, 因此我们要设法去掉绝对值符号, 将其转换为一个普通的线性初等函数, 进而可以通过借助导数来计算极值, 通常地去掉绝对值符号的方法是做平方, 但在这里我们有更简单的方式, 对于所有误分类点来说, 感知机的输出与数据的标注值或真实值(即 $y$) 的符号是相反的, 即 $f \cdot y \lt 0$ 对于任意误分类点恒成立, 因此对所有误分类点, 我们有

$$(\vec \omega \cdot \vec x_i + b) \cdot y_i \lt 0 \tag{2.14}$$

恒成立, 进一步我们有

$$- (\vec \omega \cdot \vec x_i + b) \cdot y_i = |\vec \omega \cdot \vec x_i + b| \cdot y_i \tag{2.15}$$

于是

$$h = - \sum_{x_i \in M} \frac{(\vec \omega \cdot \vec x_i + b) \cdot y_i}{||\vec \omega||_2} \tag{2.16}$$

我们的目标在于求得 $\vec \omega$ 和 $b$, 因此我们将上式视为 $\vec \omega$ 和 $b$ 的函数, 观察上面这个式子, 难以处理的一项分母上的 $L_2$ 范数, 它的存在使得求导的计算量变得很大, 实际上这里可以移除 $\frac{1}{||\vec \omega ||_2}$, 我们定义

$$h^{'} = - \sum_{x_i \in M} (\vec \omega \cdot \vec x_i + b) \cdot y_i \tag{2.17}$$

我们来分析为什么 $h^{'}$ 仍然可以用做损失函数, 因为感知机没有很强的约束, 就是找出分离正负样本点的超平面, 只要求找到一组解即可, 这与支持向量机不同, 感知机是求得解, 而支持向量机是求得最优解, 对于感知机来说, 损失函数是否携带 $\frac{1}{||\vec \omega ||_2}$ 参与迭代不影响算法的收敛性, 一般地, 函数 $h^{'}$ 描述的是误分类点的「函数距离」之和, 而函数 $h$ 描述的是所有误分类点到超平面的「几何距离」之和, 两者的差异在于当对 $\vec \omega 和 b$都放大或缩小相同的比例时, 函数距离会相应的放大或缩小, 而几何距离不变, 对感知机来说, 并不要求找到所有点到超平面距离和最小的解, 因此可以使用函数距离作为损失函数, 降低了计算量而不影响收敛性

至此, 我们的目标便是降低损失函数的值, 使得所有点都被正确分类, 此时损失函数取得最小值 0, 损失函数是关于 $\vec \omega$ 和常数 $b$ 的线性函数, 它具有一阶连续偏导数, 由于函数沿梯度方向的反方向下降最快, 因此我们沿着梯度的反方向来调整 $\vec \omega$ 和常数 $b$ 可以使得损失函数值的下降速率达到最大, 进而可以最快地获取一组解, 损失函数的梯度为

$$\mathbf{grad} \ h^{'} = (- \sum_{x_i \in M} y_i\vec x_i ) \cdot \vec i + (- \sum_{x_i \in M} y_i) \cdot \vec j \tag{2.18}$$

因此感知机算法的过程可以描述为

1. 采用某种策略随机选定一组初始解 $\vec \omega_0$ 和 $b_0$
2. 随机选取一个点, 计算其是否被正确分类, 即判断 $f \cdot y \gt 0$ 是否成立, 若不成立, 则该点是一个误分类点, 接着计算损失函数 $h^{'}$ 在该点的梯度, 转到 3; 若成立, 则该点是一个正确分类点, 跳过该点, 继续计算下一个点, 若所有点都已被正确分类, 则算法结束
3. 使用

$$\vec \omega \leftarrow \vec \omega - \eta (- y_i\vec x_i ) \tag{2.19}$$

$$b \leftarrow b - \eta (- y_i) \tag{2.20}$$

对权值向量 $\vec \omega$ 和常数 $b$ 进行更新, 其中 $\eta \in (0, 1]$, 设置 $\eta$ 的目的是为了控制前进的速率, $\eta$ 选取的过小, 则算法收敛地慢, 需要迭代的次数多, 若 $\eta$ 选取的较大, 则有可能跳过正确解, 更新完成后然后转到 2, 经过有限次迭代后, 我们可以获得问题的(其中一组)解

2.4 拓展

由于实数的稠密性, 感知机若有解, 则一定有无数组解, 而感知机的目标只是获取其中的任意一组解, 所有的解都可以称之为一个模型, 但这些模型之间不是等价的, 对于分类问题来说, 一个自然的目标便是最大化不同类别之间的距离, 因为若如分类距离小, 则误分类的概率就会相对变大, 在感知机的损失函数中, 我们使用函数距离来度量误分类点的偏差程度, 与此相对的, (线性)支持向量机使用更直观意义上的几何距离来度量误分类点的偏差程度, 相对于感知机, (线性)支持向量机加入了更强的约束, 最终会从所有的待定解中选择(使得分类距离最远的)唯一解, 近期会再写一篇文章详细论述支持向量机的数学原理.